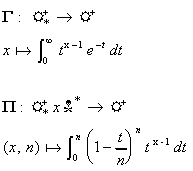
ECOLE NATIONALE

DE LA STATISTIQUE

ET DE L'ANALYSE

DE L'INFORMATION
ENSAI
INSTITUT NATIONAL DE LA STATISTIQUE ET DES études économiques


ECOLE NATIONALE DE LA STATISTIQUE

ET DE L'ANALYSE DE L'INFORMATION

______

concours d'élève titulaire de l'ENSAI

concours externe d'attaché de l'INSEE

______

MAI 1996

_____

Option A. - MATHEMATIQUES

_____

deuxième composition de mathématiques

Durée : 4 heures

______


Préambule

1. Sauf mention contraire, dans tout le problème, x désigne un réel strictement positif et n désigne un entier strictement positif.

2. On définit les applications suivantes :


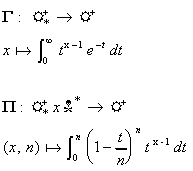
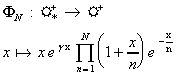
où g est une constante qu'on déterminera par la suite et N un entier strictement positif.

3. Le but de la première partie est l'étude des fonctions G, P et FN. Le but de la deuxième partie est de montrer que :

.

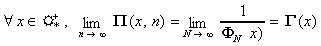Enfin, la troisième partie établit un lien entre G(x) et l'intégrale multiple :

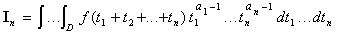avec f continue,

ai 1 (i = 1,..., n), D = .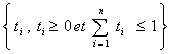

4. Toutes les parties peuvent se traiter indépendamment en admettant les résultats des parties précédentes.

I

1. Etudier l'ensemble de définition et la continuité de G(x).

Montrer que la fonction G(x) est dérivable sur 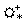, avec .

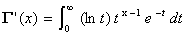2. Montrer que G(x + 1) = x.G(x). En déduire G(x) pour x N*.

3. Montrer que :

.

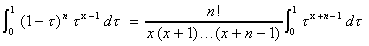4. En déduire que :

P(x, n) = .

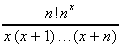5. Soit la suite (un)n N* définie par :

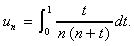
a. Calculer un.

b. Montrer que la série de terme général un converge. En déduire que :

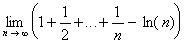existe.

On note g cette limite.

6. Soit gn(x) = 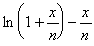, avec 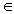N N*, N < n.

a. Montrer que si 0 x N, alors .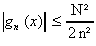

b. En déduire que la fonction S(x) = 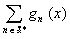existe et est continue sur .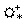

c. Montrer que S(x) est dérivable sur 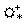et que .

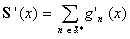d. En déduire que :

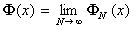
est une fonction définie, continûment dérivable sur 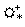avec F(1) = 1 et F'(1) = g.

II


1. Montrer que :

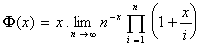
et que :

.

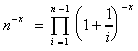2. En déduire que :

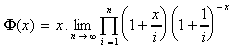
puis que :

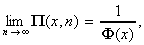
x .

3. a. Montrer que :

(1 - y)-1 e y 1 + y, 0 y < 1.

En déduire que :

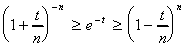, t, 0 t < n.

b. En déduire :

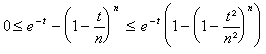, t, 0 t < n.

c. En montrant que :

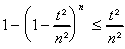, t, 0 t < n.

prouver que :

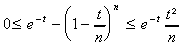, t, 0 t < n.

4. Montrer que x :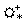

.

En déduire G'(1) en fonction de g.


III

On définit :

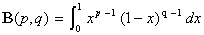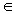
, ( p, q) x

1. a. Montrer que B( p, q) = B( p + 1, q) + B( p, q + 1) et B( p, q + 1) = 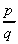B( p + 1, q).

En déduire que :

B( p, q + 1) = B( p, q).

b. Montrer que B(x, n + 1) = n-x P(x, n) et en déduire :

G(x) = .

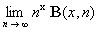2. Soient m et n deux réels, m > 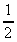, n > 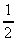et la fonction :

.

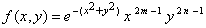a. Montrer que :

G(m)G(n) = 4.

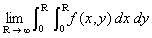b. Par un changement de coordonnées, montrer que :

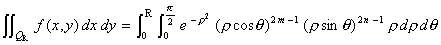
où QR est le quadrant centré à l'origine et de rayon R.

c. En déduire l'égalité :

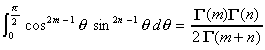
puis calculer, à l'aide de I.2. :

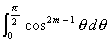, m N*.

d. Montrer que :

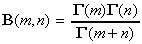
et, à l'aide du 1., généraliser ce résultat à (m, n) 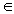( x ).

3. On définit 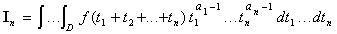, où f est continue, ai 1

(i = 1,..., n), l'intégration se faisant sur les valeurs positives telles que t1 + t2 + ... + tn 1.

On définit également pour 0 t3 1 :

.

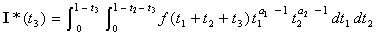a. Montrer que si t [0,1], f(t) = 1 et n = 2, on a :

.

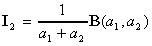b. En posant 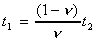, montrer que :

.

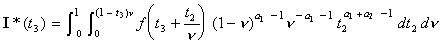c. En déduire :

.

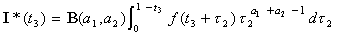d. En déduire :

.

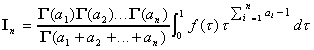Historiquement, la fonction G(x) a été d'abord développée par Euler sous sa forme intégrale, la fonction B(p, q) porte le nom d'Intégrale d'Euler de première espèce et a été développée par Euler et Legendre. Le lien avec la fonction F est dû à Weierstrass et le lien avec l'intégrale multiple In est dû à Dirichlet.