Le point de Toricelli

I. Position du problème
II. Etude d'une condition d'existence et d'unicité
III. Cas (presque) général
IV. Pour aller plus loin

---

I. Position du problème

On considère un triangle ABC d'un plan euclidien. On se propose de construire, si c'est possible, un point M tel que la somme des distances MA+MB+MC soit minimale.

II. Etude d'une condition d'existence et d'unicité

- Données :

On identifie le plan à l'ensemble C des nombres complexes: on munit le plan d'un repère orthonormé (O;u,v) et à tout point M=O+xu+yv on associe son affixe z=x+iy.
On note a, b et c les affixes de A, B et C, que l'on suppose non nulles. On se donne également trois points P, Q et R d'affixes p, q et r définies par:
p=|a|/a
q=|b|/b
r=|c|/c

- Etude du triangle PQR :

Remarquons d'abord que les point P, Q et R sont situés sur le cercle unité (c'est à dire |p|=|q|=|r|=1).

En effet, on a:
|p|=||a|/a|=|a|/|a|=1
et de même |q|=1 et |r|=1.

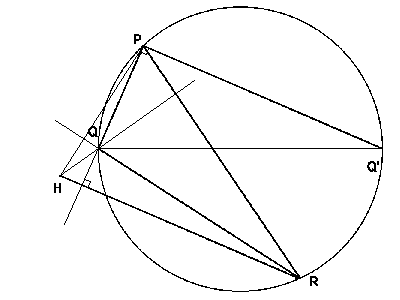
Soit H le point d'affixe h=p+q+r. Montrons que H est l'orthocentre du triangle PQR.

En effet, la définition de H par son affixe s'écrit h-r=p+q. En notant Q' le point d'affixe -q, Il vient l'égalité vectorielle H-R=P-Q'. Or Q' est le point du cercle unité diamétralement opposé à Q, donc le triangle PQQ' est rectangle en P. Les vecteurs P-Q et P-Q' sont donc orthogonaux; il en est de même des vecteurs P-Q et R-H, donc H appartient à la hauteur de PQR issue de R. On montre de même que H est un point de chacune des hauteurs de PQR; H est donc l'orthocentre de PQR.

- Etude du problème lorsque PQR est équilatéral :

Nous supposerons dans la suite du paragraphe que la relation p+q+r=0 est vérifiée.

Remarquons d'abord que la quantité S=|p(z-a)+q(z-b)+r(z-c)| ne dépend pas du choix du complexe z. En effet, on a toujours: S=|(p+q+r)z-pa-qb-rc|=|pa+qb+rc|=||a|+|b|+|c||=|a|+|b|+|c|
Or on a montré que la définition des point P, Q et R entraine l'égalité |p|=|q|=|r|=1, d'où on déduit:
S|p||z-a|+|q||z-b|+|r||z-c|=|z-a|+|z-b|+|z-c|
On a donc zC , |a|+|b|+|c||z-a|+|z-b|+|z-c|
Or, en notant M le point du plan d'affixe z, on a |z-a|+|z-b|+|z-c|=MA+MB+MCOA+OB+OC=|a|+|b|+|c|
La somme MA+MB+MC est donc minimale pour M=O.

III. Cas (presque) général

- Données du problème :

On se donne un triangle ABC dont aucun des angles ne mesure plus de 120°.
On veut trouver un repère orthonormal où les points P, Q et R définis au paragraphe II forment un triangle équilatéral.
Notons que dans un tel repère les points A, B et C sont tous d'affixe non nulle (sinon P, Q et R ne sont pas tous trois définis).

- Remarque concernant la mesure des angles :

Dans la suite de cet article, on prendra comme mesure d'un angle sa mesure "principale" en degrés (c'est à dire sa mesure en degrés dans l'intervalle [0,360], on admet les valeurs 0° et 360° pour l'angle nul). On travaillera toujours "modulo 360°", mais pas systématiquement avec des angles orientés.

- Analyse :

Supposons avoir trouvé un repère (O;u,v) convenable.

Définissons les points P, Q et R comme au paragraphe I: ce sont les points d'affixes respectives
p=|a|/a
q=|b|/b
r=|c|/c

On a |a|²=a et a0 donc |a|0 et p=/|a|
et de même q=/|b| et r=/|c|.

De plus, O est l'unique point intérieur au triangle ABC tel que les angles (OA,OB), (OB,OC) et (OC,OA) aient une mesure de 120°.
En effet, si on suppose l'existence d'un second point O' ayant cette propriété, alors O' est un point d'intersection des arcs de cercles G_C et G_B définis par G_C={M; M intérieur à ABC et (MA,MB)=120°} et G_B={M; M intérieur à ABC et (MA,MC)=120°}. Or ces arcs de cercles sont des parties respectives de deux cercles distincts (le premier contient B, pas le second, car on a supposé (BA,BC)<120°), sécants en A et O; et le point A est exclu, donc O=O'.

- Construction d'un point O convenable :

C'est à dire: construisons un point O intérieur à ABC, tel que l'on ait l'égalité des angles: (OA,OB)=(OB,OC)=(OC,OA)=120°.
On supposera dans la suite que le triangle ABC est direct afin de pouvoir travailler avec les angles orientés.

Construisons trois triangles équilatéraux ABC', AB'C et A'BC extérieurs au triangle ABC. Leurs trois cercles circonscrits, notés respectivement G_C, G_B etG_A, ont un point commun O, qui est intérieur au triangle ABC.
Pour montrer cette propriété, noous allons d'abord montrer que deux quelconques des trois cercles, par exemple G_C et G_B, sont sécants, et que leur second point d'intersection (le premier étant A) est intérieur à l'angle (AB,AC). Puis nous allons montrer que ce second point d'intersection appartient au troisième cercle G_A.

1. G_C et G_B ont A pour point commun. Ils sont donc soit tangents, soit sécants. Supposons-les tangents et cherchons une contradiction.
   Le triangle ABC' est équilatéral, donc la tangente T_C à son cercle circonscrit G_C au point A est parallèle à la droite (BC') (en effet, la hauteur issue de A est également le support d'un diamètre de G_C, et elle est donc orthogonale à T_C). Notons I_C un point de T_C intérieur à l'angle (AB,AC); alors les angles (AB,AI_C) et (BA,BC') sont de même mesure; on a donc (AB,AI_C)=60°.
   Mais si les cercles G_B et G_C sont tangents, alors T_C est également tangente à G_B, et un raisonnement similaire au précédent nous donne (AI_C,AC)=60°; d'où d'après la relation de Chasles (AB,AC)=120°, ce qui contredit l'hypothèse (AB,AC)<120°.
   Le cercles G_B et G_C sont donc sécants en A et un second point; notons O ce point.
2. Montrons maintenant que O est intérieur à l'angle (AB,AC).
   O est un point du cercle G_C, donc il appartient au demi-plan de frontière T_C contenant C'. On a donc (AB,AO)<60° ou (AB,AO)>240°, suivant que O est respectivement intérieur ou extérieur à l'angle (AB,AC), et de même (AO,AC)<60° ou (AO,AC)>240°. Le cas où (AB,AO)>240° et (AO,AC)>240° est impossible, car on aurait alors par la relation de Chasles (AB,AC)>120°. D'autre part, si (AB,AO)>240° et (AO,AC)<60°, alors la relation de Chasles nous donne (AB,AC)]240,300[, ce qui est contraire à l'hypothèse (AB,AC)<120°; de même si (AB,AO)<60° et (AO,AC)>240°.
   Finalement, il ne reste que la dernière possibilité: (AB,AO)<60° et (AO,AC)<60°, c'est à dire que le point O est intérieur à l'angle (AB,AC).
3. Montrons enfin que le point O est un point du cercle G_A.
   O est un point de G_C, situé dans le demi-plan ouvert de frontière (AB) ne contenant pas C', donc on a (OA,OB)=120°. De même on a (OC,OA)=120°. La relation de Chasles nous donne donc (OB,OC)=120°. Un raisonnement analogue à celui de l'étape précédente nous permet alors de conclure que le point O est intérieur à l'angle (BC,BA), et donc que O est un point du demi-plan ouvert de frontière (BC) ne contenant pas A'; or les points M de ce demi-plan tels que (MB,MC)=120° sont situés sur le cercle G_A; O est donc un point de G_A.
4. De plus, l'étape 2 permet de conclure que le point O est intérieur à chacun des angles (AB,AC), (BC,BA) et (CA,CB), donc que O est intérieur au triangle ABC.

Récapitulons: Nous avons montré que les cercles circonscrits aux triangles équilatéraux A'BC, AB'C et ABC' sont concourants, et que le point de concours O est un point intérieur au triangle ABC, tel que (OA,OB)=(OB,OC)=(OC,OA)=120°. O est donc, d'après l'analyse précédente, un minimum de l'application d du plan dans R₊ définie par d(M)=MA+MB+MC.

- Construction pratique :

Etant donné un triangle ABC, on construit extérieurement à ABC trois triangles équilatéraux A'BC, AB'C et ABC'. On trace leurs cercles circonscrits, qui sont concourants. Leur point de concours est le point recherché; c'est le point de Toricelli du triangle ABC.

IV. Pour aller plus loin

- Existe-t-il d'autres minima de la somme MA+MB+MC?

- Que se passe-t-il si l'un des angles du triangle ABC est supérieur à 120°?

Le triangle PQR de la partie II ne peut pas être équilatéral (ça se démontre, mais je n'ai pas encore retrouvé comment...). La construction étudiée dans cet article n'est donc plus valable.