Suite de fonction
Soit E un espace vectoriel normé de dimension finie.
I) Convergence des suites de fonctions
Soit (fn)n une suite de l'espace vectoriel des fonctions bornées.
(fn)n converge uniformément vers f si et seulement si " e>0, $ n0Î n, " n>n0, | | fn - f| | <e
Dans la pratique, on utilise la définition suivante :
(fn)n converge uniformément vers f si et seulement si sup | | fn - f| | est borné et tend vers 0 quand n tend vers l'infini.
Pour étudier la convergence simple, on fixe x et on fait tendre n vers l'infini. Par exemple :
fn(x) = x + exp(-nx) converge vers f(x) = x pour x³ 0, diverge pour x<0.
Pour étudier la convergence uniforme, on majore la suite | | fn - f | | par une suite indépendante de x et qui tend vers 0 quand n tend vers l'infini (cela équivaut à un passage au sup). Exemple :
| fn (x) - f(x) | = | x + exp(-nx) - x | = exp(-nx) £ exp(-na) pour x³ a, a>0.
Donc (fn) converge uniformément vers f sur [a, +¥ [,a>0 (mais pas sur [0, +¥ [).
La convergence uniforme entraîne la convergence simple.
Il faut toujours commencer par étudier la convergence simple puisque l'étude de la convergence uniforme impose de connaître f.
Si (fn) converge uniformément vers f sur A1 et A2 alors (fn) converge uniformément vers f sur A1È A2. On peut généraliser à une union finie.
II) Les théorèmes généraux
fn : AÌ r® r
- (ln)n converge vers l
- la limite de f en a existe et vaut l
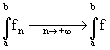
- (f 'n)n converge simplement vers une fonction g sur A, la convergence étant uniforme sur tout compact inclus dans A
- $ aÎ A, (fn(a))n converge
alors : -(fn) converge simplement vers une fonction f sur A, la convergence étant uniforme sur tout compact inclus dans A
- f est C1 sur A et f ' = g
FIN