Développements en série entière usuels

 

 

 

sin (x) = R = +¥

cos (x) = R = +¥

sh (x) = R = +¥

ch (x) = R = +¥

 

 

1/(1-x) = R = 1

1/(1+x) = R = 1

ln (1+x) = R = 1 (valable en x = 1)

ln (1-x) = - R = 1

exp (x) = R = +¥

 

 

(1+x)a = 1 + R = 1 si aÏ n, R = +¥ sinon

Arctan (x) = R = 1

Arcsin (x) = x + 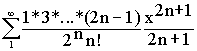R = 1

 

 

Pour les fractions, le rayon de convergence est égal au plus petit des pôles de la fraction donc une fraction est développable en série entière si et seulement si 0 n'est pas un pôle de la fraction.

 

Première version : 01/03/98
Auteur : Frédéric Bastok e-mail :fred_bastok@bugss.org)
Source :
Relecture : Aucune pour l'instant