k = r ou c

(u_n)_n Î kⁿ

On pose S_n = . u_n est le terme général de la série et S_n est la somme partielle d'ordre n.

On dit que la série å u_n converge si et seulement si la suite (S_n)_n converge . Sinon la série diverge.

Si la série converge, la limite de la suite (S_n)_n est appelée la somme de la série et est notée

Condition nécessaire de convergence : si la série å u_n converge alors la suite (u_n) converge vers 0.

Soit n'Î n

est la série reste d'ordre n' de la série å u_n. Si la série converge, on appelle reste d'ordre n' (noté R_n') la somme de la série reste.

Si on modifie un nombre fini de termes de la série, on ne modifie pas sa nature mais on modifie sa somme.

On dit que la série å u_n converge absolument si et seulement si la série å | u_n| converge.

Théorème : si la série converge absolument alors elle converge.

L'ensemble des séries convergentes forment un k -espace vectoriel.

La somme de deux séries divergentes peut être convergente.

Les séries peuvent aussi servir à étudier les suites (on parle alors de série associée à une suite).

Pour étudier la convergence de la suite (x_n)_n, on pose : y_n = x_n - x_n-1 pour n>0 et y₀ = x₀

On a alors le résultat : (x_n)_n converge Û å y_n converge

Théorème : Une série à termes positifs convergent si et seulement si la suite de ses sommes partielles est majorée.

Pour que l'on puisse parler de séries à termes positifs, les séries doivent être réelles.

1) Critère de convergence

Dans tous les théorèmes suivant, on suppose que (u_n)_n et (v_n)_n sont des suites dont les termes sont de signe constant à partir d'un certain rang.

• Convergence par inégalité

On suppose qu'à partir d'un certain rang : 0 (ou v_n ) alors

- si la série å v_n converge, å u_n converge

- si la série å u_n diverge, å v_n diverge.

• Convergence par équivalence

On suppose que : u_n ~ v_n et que (u_n) ou (v_n) est à termes positifs (ou négatifs) à partir d'un certain rang alors les séries å v_n et å u_n sont de même nature.

• Convergence par prépondérance

On suppose que : u_n << v_n et que (v_n) est à termes positifs (ou négatifs) à partir d'un certain rang (aucune hypothèse sur le signe de (un)) alors si å v_n converge alors å u_n converge.

Si de plus (u_n) est à termes positifs (ou négatifs) à partir d'un certain rang alors si å u_n diverge, å v_n diverge.

• Convergence par comparaison aux intégrales

Si le terme général de la série peut s'écrire sous la forme f (n) où f est une fonction continue monotone alors on peut encadrer la série par des intégrales impropres.

Par exemple : 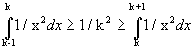que l'on trouve en considérant les aires

d'où : 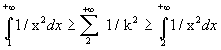après avoir prouvé la convergence des intégrales. Si on peut trouver un équivalent des intégrales ou les calculer, cela permet parfois de prouver la convergence de la série. Mais on s'en sert plus pour trouver des équivalents dans le cadre des séries de fonctions.

le théorème suivant peut être utile :

Si f est une fonction continue décroissante sur [n', +¥ [ et f(x) alors la série et l'intégrale sont de même nature.

• Règle de D'Alembert

- Si il existe k dans [0, 1[ tel que à partir d'un certain rang: 0u_n+1/u_n alors la série å u_n converge.

- Si u_n+1/u_nalors å u_n converge si l<1

diverge si l>1

aucune conclusion si l= 1

On rappelle qu'en général on ne peut pas sommer les relations d'équivalence et de prépondérance : f₁ g₁ et f₂ g₂ n'entraîne pas f₁ + f₂g₁ + g₂ (valable aussi pour )

Théorème :

On suppose que (v_n)_n est à termes positifs à partir d'un certain rang et que u_n << v_n ou u_n ~ v_n

- Si å v_n converge alors å u_n converge et quand n tend vers +¥ , (de même pour la prépondérance).

- Si å u_n diverge alors å v_n diverge et quand n tend vers +¥ , (de même pour la prépondérance).

Théorème de Césaro :

Si (u_n)_n converge vers l alors converge vers l.

Pour l'étude des sommes de Riemann, on regardera le chapitre sur les intégrales.

3) Convergence absolue

Dans ce paragraphe, on considère des séries à valeurs dans c du moins pour (u_n)_n

- Si | u_n| v_n à partir d'un certain rang et si å v_n converge alors å u_n converge absolument.

- Si u_n ~ v_n et si å v_n converge absolument, alors å u_n converge absolument.

- Si u_n << v_n et si å v_n converge absolument, alors å u_n converge absolument.

Ces relations ne permettent pas de montrer la divergence de å u_n même si å | u_n| diverge.

Une série convergente non absolument convergente est dite semi-convergente.

Les résultats vus avec les séries à termes positifs ne s'appliquent pas.

1) Série alternée

Théorème :

Soit une série de terme général : u_n = (-1)ⁿ a_n où (a_n) est une suite de termes positifs décroissante et tendant vers 0. Dans ce cas, å u_n converge.

Une alternance de signe ne suffit pas pour appliquer le théorème.

Propriétés : - la somme de la série est comprise entre 2 sommes partielles consécutives.

- le reste est majoré en valeur absolue par le 1^er terme négligé. Le signe du reste d'ordre n est celui du terme d'indice n+1.

2) Parenthèsage

Cela consiste à placer judicieusement des parenthèses dans une série pour pouvoir faire des

" paquets " .On l'utilise souvent avec les parties entières ou . Le parenthèsage est différent de la permutation des termes. Il faut essayer de s'en servir le moins possible car ça n'est pas évident ! Pour plus de renseignements, ouvrir un livre sur les séries.

Etant données 2 séries å u_n etå v_n, on appelle série produit la série de terme général w_n :

w_n =

Théorème : Si les séries convergent absolument alors la série produit converge absolument et sa somme est le produit des sommes.

Les séries suivantes sont divergentes :

• å ln (1+1/n) (par télescopage)
• å 1/n

Les séries suivantes sont convergentes :

• å 1/n!
• å (-1)ⁿ/n

Les séries de référence usuelles sont (on essaye de comparer les séries à celles-ci dans les exercices) :

• série de Riemann : la série å 1/n^a ,aÎ r, converge si et seulement si a >1
• série de Bertrand : la série å 1/(n^a ln^b n), (a, b)Î r´ r, converge si et seulement si a>1 ou a=1 et b>1