Séries de fonction
I) les différentes convergences
Soit E un espace vectoriel normé complet, A une partie d'un espace vectoriel normé.
On pose : " n, un : A® E. On s'intéresse à la série de fonctions å un et on pose :
"
xÎ
A, Sn(x) = ![]() (somme partielle d'ordre n).
(somme partielle d'ordre n).
(Sn) est une suite de fonctions donc on va pouvoir appliquer la théorie du chapitre correspondant.
La convergence simple (resp. uniforme) de la série [un] équivaut à la convergence simple (resp. uniforme) de la suite (Sn).
Proposition : si la série [un] converge uniformément sur A alors la suite (un) converge
uniformément vers 0 sur A.
Remarque : lorsqu'une série converge, on ne précise pas vers quoi puisque qu'elle converge
vers sa somme.
Proposition : [un] converge uniformément sur A si et seulement si [un] converge simplement et
(Rn) converge uniformément vers 0 sur A. (§)
On peut maintenant donner la définition d'un nouveau type de convergence : la convergence normale.
Définition : on note | | un | | ¥ =sup | | un | | s'il existe dans r.
[un] converge normalement sur A si et seulement si " n, un est bornée sur A et
[ | | un | | ¥ ] converge.
Pour prouver la convergence normale d'une série, on majore (en valeur absolue) le terme général de la série par le terme général d'une série convergente indépendante de x.
Exemple : | cos(nx)/n2 | £ 1/n2 . Or [1/n2] est une série convergente, indépendante de x d'où la
convergence normale de [cos(nx)/n2] ( ici sur r).
Si une série converge normalement, alors elle converge uniformément, simplement et absolument.
En conséquence pour prouver la convergence uniforme d'une série, on cherche à montrer la convergence normale sauf si la série est alternée.
Théorème de convergence uniforme pour les séries alternées :
Ce sont les séries du type [ (-1)n un].
On suppose que " xÎ A, (un(x)) est suite décroissante tendant vers 0.
Alors [ (-1)n un] converge simplement sur A.
Pour étudier la convergence uniforme :
On rappelle que " xÎ A, " n, | Rn(x) | £ un+1(x)
On essaye de majorer un+1 par une suite indépendante de x et tendant vers 0 ce qui
permet d'appliquer la proposition (§).
II) Propriétés de la somme d'une série
On pose S(x) = ![]()
- [ln]n converge
- la limite de S en a existe et vaut ![]()
sur [a, b] alors 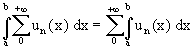
- [u 'n]n converge simplement vers une fonction g sur A, la convergence étant uniforme sur tout compact inclus dans A
- $ aÎ A, [un(a)]n converge
alors : -[un] converge simplement sur A, la convergence étant uniforme sur tout compact
inclus dans A
- S est C1 sur A et S '(x) = ![]()
FIN