E désigne un espace vectoriel sur r ou c.

Dans le cas réel :

Définition :

Un produit scalaire sur E est une forme bilinéaire définie symétrique positive.

i.e. : - c'est une forme : E² ® r

(x, y) ® <x, y>

- bilinéaire : " a, a'Î r, " x, x', y, y'Î E,

<ax + a'x', y> = a <x, y> + a' <x', y>

<x, ay + a'y'> = a <x, y> + a' <x', y>

- définie : " xÎ E, <x, x> = 0 Þ x = 0

- symétrique : " x, yÎ E, <x, y> = <y, x>

- positive : " xÎ E, <x, x> ³ 0

Dans le cas complexe :

Définition :

Un produit scalaire sur E est une forme sesquilinéaire hermitienne définie positive.

i.e. : - c'est une forme : E² ® c

(x, y) ® <x, y>

- sesquilinéaire : " a, a'Î c, " x, x', y, y'Î E,

<ax + a'x', y> = <x, y> + <x', y> (semi - linéarité par rapport à la 1^er variable)

<x, ay + a'y'> = a <x, y> + a' <x', y> ( linéarité par rapport à la 2^eme variable)

- hermitienne : " x, yÎ E, <x, y> =

- positive : " xÎ E, <x, x> ³ 0

- définie : " xÎ E, <x, x> = 0 Þ x = 0

| | x | | ² = <x, x> est une norme sur E.

| | x + y | | ² = | | x | | ² + 2 <x, y> + | | y | | ²

<x, y> = ( | | x + y | | ² - | | x - y | | ² )/4 identité de polarisation

| | x + y | | ² + | | x - y | | ² = 2 ( | | x | | ² + | | y | | ² ) identité du parallélogramme

E préhilbertien, x, yÎ E.

• Inégalité de Cauchy - Schwartz : | <x, y> | £ | | x | | . | | y | | avec égalité si et seulement si (x, y) est liée.
• Inégalité de Mintkowski : | | x + y | | £ | | x | | + | | y| | avec égalité si et seulement si x et y sont positivement colinéaires.

L'application x ® <x, x>^1/2 est une norme sur E. C'est la norme associé au produit scalaire.

Définition :

Si x et y sont deux vecteurs de E, x et y sont dits orthogonaux si et seulement si <x, y> = 0.

Propriétés :

- x ^ x Û x = 0

- " yÎ E, x ^ y Û x = 0

- | | x + y | | ² = | | x | | ² + Re <x, y> + | | y | | ²

Théorème de Pythagore :

x ^ y Þ | | x + y | | ² = | | x | | ² + | | y | | ²

La réciproque est fausse dans le cas complexe, vraie dans le cas réel.

Définition :

L'orthogonal de A, noté A^ ,où A est une partie de E, est {xÎ E / " aÎ A, x^ a}.

A ^ B Û " xÎ A, " yÎ B, x ^ y.

Si AÌ B, alors B^ Ì A^ .

On peut alors définir la notion de base orthogonale (les vecteurs de base sont orthogonaux entre eux) et de base orthonormale (les vecteurs sont en plus de norme 1).

Proposition :

Une famille orthogonales ou orthonormales de vecteurs non nuls est libre.

L'existence d'une famille orthonormale est assurée en dimension finie grâce au procédé de Gramm - Schmidt.

Définition :

Si A est un sous - espace vectoriel de dimension finie de E alors A Å A^ = E.

A^ est le supplémentaire orthogonal.

On peut aussi définir la projection orthogonale sur A P_A par :

" xÎ E, P_A(x) = où (e₁, ..., e_n) est une base de A.

... et la distance d'un vecteur à une sous - espace de dimension finie par :

d (x, A) = | | x - P_A(x) | | qui est un minimum stricte.

Enfin, en dimension finie, on a aussi : - (A + B) ^ = A^ Ç B^

- (A Ç B) ^ = A^ + B^

Définition :

L'espace de Dirichlet, noté D, est l'espace vectoriel des fonctions continues par morceaux de

r ® c, 2p - périodique et telle que : " x, f(x) = (f(x⁺) + f(x ^-))/2.

Si fÎ D, l'idée est d'approcher f par des polynômes trigonométriques i.e. de la forme exp(inx).

Toute la théorie repose le produit scalaire et la projection orthogonale.

On pose c_k(f) = .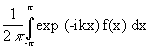

(c_k(f))_k est la famille des coefficients de Fourier de f.

La somme d'ordre n de la série de Fourier est :

S_n(f) = c₀(f) +

ce qui peut encore s'écrire, en passant à des réels (c'est l'expression qu'on utilise en général) :

S_n(f) = a₀(f) +

avec : a₀(f) =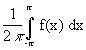

" k³ 1, a_k(f) =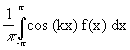

et b_k(f) =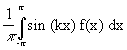

Si f est paire, tous les b_k sont nuls. Si f est impaire, tous les a_k sont nuls.

Formule de Parseval : fÎ D

| c₀(f)| ² + =

ou : | a₀(f)| ² + =

Théorème de Riemann - Lebesgue :

a_k(f) ® 0 et b_k(f) ® 0 quand k ® +¥ .

Théorème de Dirichlet :

Soit fÎ D i.e. continues par morceaux de r ® c, 2p - périodique et telle que :

" x, f(x) = (f(x⁺) + f(x ^-))/2.

Et vérifiant de plus : f est C¹ par morceaux.

Alors (S_n(f))_n converge simplement vers f sur r.

On dit que f est somme de sa série de Fourier :" x, f(x) = a₀(f) + .

Théorème de convergence normale :

Si f est 2p - périodique, continue sur r et C1 par morceaux alors la série de Fourier converge normalement sur r et sa somme est f.

On peut étendre les séries de Fourier à des fonctions de période T quelconque en posant :

c_k(f) = ce qui revient à faire partout la permutation :

2p k/T à la place de k. Les théorèmes sont alors les même.

On peut aussi étendre la théorie à des fonctions non périodiques mais cela sort du niveau de ce cours !