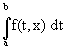Soit f : [a, b] X A ® E où A est une partie d'un espace vectoriel normé de dimension finie.

On pose : g(x) = 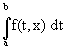sous réserve d'existence.

Théorèmes :

- si pour xÎ A, t f(t, x) est continue par morceaux sur [a, b] alors g existe.

- si f est continue sur [a, b] X A alors g est continue sur A.

Attention : il s'agit de la continuité au sens des fonctions de plusieurs variables et on

rappelle que la continuité partielle n'entraîne pas la continuité.

- si g existe et est continue sur A, si ¶ f/¶ x existe et est continue sur [a, b] X A alors g est C¹ sur A et " xÎ A, g'(x) = 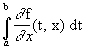. Il ne faut pas croire que si g est dérivable sans les hypothèses du théorème alors g' se calcule par la formule donnée. Par récurrence, on définit les dérivées successives ... ou on utilise le théorème suivant.

- si f, ¶ f/¶ x, ¶ ²f/¶ x², ..., ¶ ⁿf/¶ xⁿ existe et sont continues sur [a, b] X A alors g est Cⁿ sur A et " k£ n : g^(k)(x) =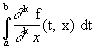

- Théorème de Fubini :

f : [a, b] X [c, d]® E continue sur le pavé.

Alors 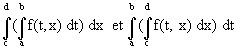existent et sont égales.

On va étudier un exemple en l'absence de théorie ( du moins au programme de Math. Spé.) tiré d'un sujet d'oral du concours Mines-Ponts. L'idée est de considérer une suite de fonction où n est à l'une des bornes (voire les 2 si l'intégrale est doublement impropre) pour pouvoir appliquer les théorèmes précédents puis appliquer la théorème de dérivation des suites de fonction.

Soit f : x 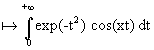. Etudier f.

® - ensemble de définition : " xÎ r, | exp(-t²) cos (xt) | £ exp(-t²) donc la convergence absolue de l'intégrale en résulte. f est définie sur r.

- posons g(x, t) = exp(-t²) cos(xt) et pour n³ 1, f_n(x) =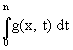

- g est continue sur r X [0, n], admet une dérivée partielle par rapport à x continue sur

cette même bande avec ¶ g/¶ x = - t.exp (-t²) sin (xt) . Par conséquent, f_n est C¹ sur r et

f '_n(x) =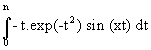

Si on pose h(x) = 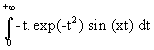(il ne faut pas oublier d'en vérifier l'existence qui

est ici triviale - négligeabilité devant 1/t²), on a :

" xÎ r, | f 'n(x) - h(x) | = | | £

£

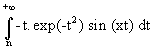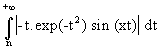
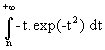
Or le dernier terme est indépendant de x et tend vers 0 quand n tend vers l'infini comme

reste d'une intégrale convergente donc (f '_n)_n converge uniformément sur r vers h (la

convergence simple est évidente) ce qui prouve que f est de classe C¹ sur r et que

f '(x) = h(x). On prouve facilement que f est C¥ et ici on peut même expliciter f grâce à

une équation différentiel du 1^er ordre mais c'est une autre histoire... .

Remarque : ici on avait la convergence uniforme sur r tout entier mais la convergence

uniforme sur tout compact suffit.