E est un espace vectoriel de dimension finie.

f : [a, b[® E avec bÎ rÈ {+¥ }, f continue par morceaux sur [a, b[.

Définition :

On dit que existe (ou converge) si et seulement si a une limite finie lorsque x® b^-.

Sinon, l'intégrale diverge.

Propriétés : - cÎ ]a, b[

existe si et seulement si existe et si elles existent on peut appliquer la relation de Chasles. La nature et la valeur de l'intégrale ne dépendent pas de c.

- Si f(x) ® l quand x ® + ¥ et si l ¹ 0, alors diverge.

- Si converge et si f a une limite en +¥ , alors cette limite est nulle.

- Si F est une primitive de f, converge si et seulement si F a une limite en b.

- L'ensemble des intégrales convergentes est un espace vectoriel.

- La somme de 2 intégrales convergentes (resp. la somme d'une convergente et d'une divergente) converge (resp. diverge). On ne peut pas conclure sur la somme de 2 divergentes.

Définition :

On dit que converge absolument si et seulement si converge.

Si l'intégrale converge, alors elle converge absolument.

Pour la même fonction f avec de plus f ³ 0, converge si et seulement si est majorée.

On a les même résultats si f £ 0 (l'important étant le signe constant).

On suppose que g ³ f ³ 0 au voisinage de b, où g est continue par morceaux sur [a, b[.

Si converge alors converge.

Si diverge alors diverge.

On suppose f ~ g et g ³ 0 au voisinage de b. Les 2 intégrales sont alors de même nature.

Siconverge alors converge et ~ au voisinage de b.

Si diverge alors diverge et ~ au voisinage de b.

On suppose f << g et g ³ 0 au voisinage de b. Les 2 intégrales sont alors de même nature.

Siconverge alors converge et >> au voisinage de b.

Si de plus f ³ 0,si diverge alors diverge et >> au voisinage de b.

Toutes les règles précédentes sont valables en remplaçant la convergence par de la convergence absolue.

5) Comparaison aux séries

(b_n)_nÎ [a, b[ⁿ tel que b_n® b, (b_n) strictement monotone alors

converge si et seulement si la série å converge.

Le changement de variable et l'intégration par parties sont valables pour toutes les fonctions.

Si on fait un changement de variable C¹ et strictement monotone, alors l'intégrale du départ et la nouvelle intégrale sont de même nature.

En intégrant par parties : f, g C¹

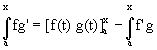
Si 2 des 3 quantités ont une limite finie quand x tend vers b alors la 3^eme aussi.

Il est conseillé de refaire tout le raisonnement plutôt que d'appliquer le résultat.

- intégrale de Riemann :

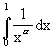converge si et seulement si a < 1.

converge si et seulement si a > 1.

- intégrale de Bertrand :

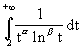converge si et seulement si : a > 1 ou a = 1et b>1.

- intégrale exponentielle :

converge (car e^-t<<1/t²).