Proposition :
G est C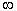 , avec G(n)
=
, avec G(n)
= 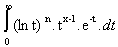
Démonstration :
Posons fn(x) =  .
.
On a alors, pour tout n, fn est C et pour tout entier
k, fn(k)(x) = 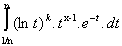
Il est alors évident que fn converge simplement
vers G et même plus généralement,
quelque soit k, fn(k) converge simplement
vers Gk =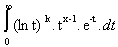 .
.
Nous allons maintenant montrer qu'il y a convergence uniforme
sur tout segment [a, b] R+*.
Soit k  N.
N.
Soit e > 0.
Soient a, b R, tels que 0 < a < b.
 x
x  [a, b],
|fn(k)(x) - Gk(x)|
[a, b],
|fn(k)(x) - Gk(x)|
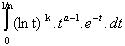 +
+ 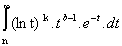 .
.
Par convergence simple de fn(k)(a) vers
Gk(a), il vient :
N1  N /
n > N1,
N /
n > N1, 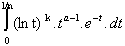 <
< 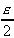 .
.
Par convergence simple de fn(k)(b) vers
Gk(b), il vient :
N2  N /
n > N2,
N /
n > N2, 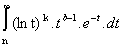 <
< 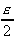 .
.
Posons N3 = Max(N1, N2).
Il vient alors :
n > N3, x  [a, b],
|fn(k)(x)
- Gk(x)| < e.
[a, b],
|fn(k)(x)
- Gk(x)| < e.
La convergence uniforme est donc démontrée.
Il s'en suit que G0 (=
G) est C, et donc que G(n)
= 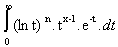 .
.
(Voir le cours sur les suites de fonctions)
Graphe de G.
G est convexe
G est logarithmiquement convexe
Nous allons donc montrer que ln(G)
est convexe
- Proposition
G(x+1) = x.G(x).
- Démonstration
On a G(x+1) = 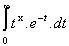 =
= 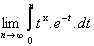 .
.
Si on intègre par partie 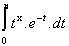 , il
vient :
, il
vient :
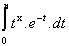 =
= 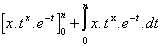
= x.nx.e-n + x. 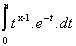
Si on passe à la limite, il vient :
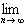 x.nx.e-n =
0
x.nx.e-n =
0
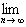
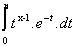 = G(x)
= G(x)
D'où G(x+1) = 0 + x.G(x)
- Corollaire :
On en déduit G(n) = (n-1) !
pour n > 0 N :
En effet, en appliquant le résultat précédent,
il vient
n N*, G(n) =
G(1).n !
Or G(1) = 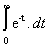 = 1
= 1
D'où le résultat.
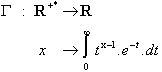
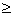 1, il n'y a pas de problème d'existence de l'intégrale.
1, il n'y a pas de problème d'existence de l'intégrale.
 ]0, 1[, on a alors :
]0, 1[, on a alors :
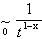
 ]0, 1[, donc l'intégrale converge en 0 par comparaison
aux intégrales de Riemann.
]0, 1[, donc l'intégrale converge en 0 par comparaison
aux intégrales de Riemann. R+*.
R+*.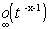 , d'où
tx-1.e -t <<
, d'où
tx-1.e -t << 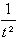 .
.
 sur R+*.
sur R+*.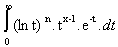
 .
.
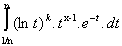
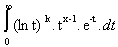 .
.
 x
x 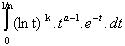 +
+ 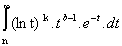 .
.
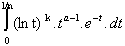 <
< 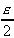 .
.
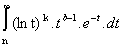 <
< 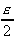 .
.
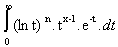 .
.
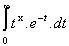 =
= 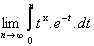 .
.
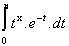 , il
vient :
, il
vient :
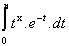 =
= 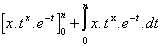
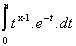
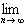 x.nx.e-n =
0
x.nx.e-n =
0
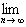
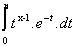 = G(x)
= G(x)
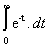 = 1
= 1