I. Introduction
II. Etude de deux cas particuliers
- Zêta de deux
- Zêta de quatre
III. Cas général
- Notations
-Etudes des fonctions C et S
- Formule de Zêta de 2m
- Simplification
- Calcul effectif

Cet article a pour but de trouver une formule donnant formellement la valeur exacte de la fonction Zêta en certain points : les entiers pairs strictement positifs.

Il s'agit de la généralisation de la méthode utiliser pour calculer Zêta de deux en utilisant la théorie des séries de Fourrier.

Ouvrir l'article sur le calcul de Zêta de deux

II. Etude de deux cas particuliers

- Zêta de deux

On étudie la fonction continue, 2-périodique, dont la restriction sur [-,+] coïncide avec la fonction valeur absolue.

La fonction est donc paire, les coefficients b_n de Fourrier sont donc nuls, le calcul des coefficients a_n donne :

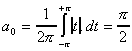
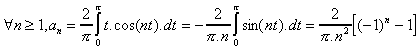
donc pour n paire, le coefficient est nul.

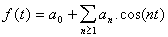
On en déduit :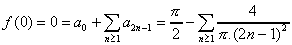

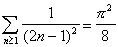
On observe alors que : 1

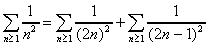
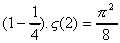
On aboutit donc au résultat suivant :

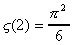
- Zêta de quatre

On procède par analogie, en étudiant cette fois la fonction continue, 2-périodique, dont la restriction sur [-,+] coïncide avec la fonction valeur absolue au cube.

La fonction est toujours paire.

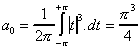
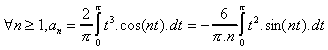
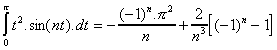
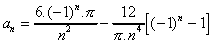
Les deux séries partielles convergent absolument (séries de Riemann), on peut

donc écrire :

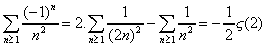
et

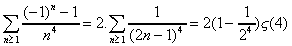
Donc :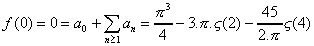

On aboutit alors à :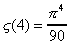

III. Cas général

- Notations

Nous allons garder n pour les calculs, on essaye donc de calculer Zêta de 2m. Pour cela, étudions, par analogie avec les précédents exemples, la fonction continue, 2-périodique, dont la restriction sur [-,+] coïncide avec la fonction 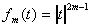. Les coefficients b_n de Fourrier sont toujours nuls. On appelle 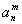les coefficients a_n de Fourrier de cette fonction.

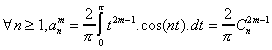
-Etudes des fonctions C et S

On définit :

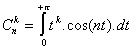
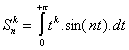
On vérifie aisément que :

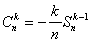
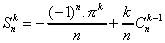
Il s'ensuit les relations de récurrence directes :

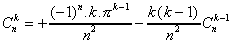
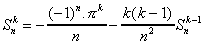
On défini alors, pour simplifier (Si j'ose dire !)

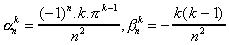
Ce qui donne

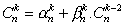
On note par ailleurs que :

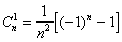
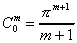
On défini alors l'égalité L_k par :

L_k :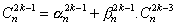

On veut que, en additionnant ces égalités pour k variant de 3 à m, il y ait télescopage, on définit donc le coefficient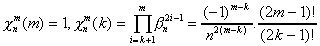

et on fait le télescopage

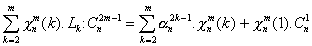
On simplifie les coefficients :

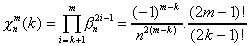
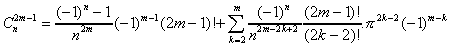
On opère un changement d'indice l=m-k+1 pour la somme :

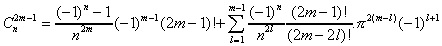
Remarquez que l'on a regroupé ce qui dépends de n.

Là, on a besoin d'une petite formule facile à démontrer :

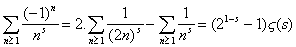
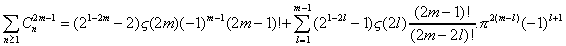
On a donc trouver une expression de ls somme des C(n,2m-1) qui va nous permettre de calculer la somme des coéfficients de Fourrier de la fontion étudiée.

- Formule de Zêta de 2m

Si on se rappelle bien, on avai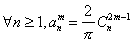t et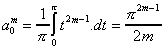

On a alors :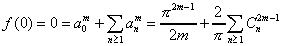

Ce qui donne, d'après le paragraphe précédent :

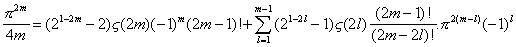
On obtient alors la formule donnant Zêta de 2m en fonction des Zêta de 2l, l<m :

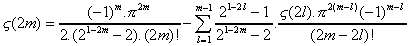
On vérifie aisemment qu'en faisant m=1, ou m=2 on obtient bien 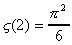et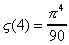

On remarque également qu'on a ainsi prouvé que 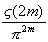est un rationnel, c'est en effet vrai au rang 2 et 4, d'après l'introduction, et par récurrence de deuxième espèce pour le cas général.

- Simplification

Cette formule, bien qu'exact, n'est pas très pratique à utiliser. Voyons comment en simplifier l'utilisation.

On peut tirer de la formule, la suivante :

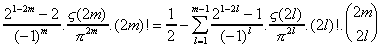
et donc, en posant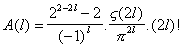

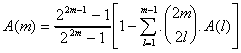
Admettons que les A(m) sont plus facile à calculer.

Si quelqu'un trouve quelque chose de plus à faire, il a le droit de m'écrire, mon adresse est à la fin de l'article !

- Calcul effectif

J'ai utilisé Maple V, pour effectuer les calculs. Donnons déjà les premières valeurs de Dzêta(2m) à votre légitime impatience :

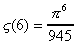
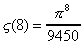
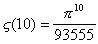
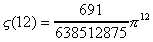
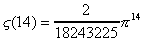
Comme on le voit, Zêta(2m) n'est pas de la forme pi^2m/a avec a entier.

On sait d'après l'introduction que A(1)=1/6.

Les fonctions (Maple) suivantes :

f:=proc(m) 2^(1-2*m)-1 end;C:=proc(n,p) n!/(p!*(n-p)!) end;

B:=proc(m) sum('C(2*m,2*l)*a[l]', 'l'=1..(m-1)) end;

D:=proc(m) f(m)/(f(m)-1)*(1/2-B(m)) end;

permettent de calculer le coéfficient A(m) en fonctions des précédents, qui sont stockés dans un tableau a[].

(Par exemple, ici, vous avez les 7 premières valeurs)

a:={1/6,-7/30,31/42,-127/30,2555/66,-1414477/2730,57337/6};

La fonction d :

d:=proc(l) D(l)*pi^(2*l)*(-1)^l/f(l)/(2*l)! end;

permet alors de calculer Zêta(2m)=d(m)

Le programme complet sous Maple V donne donc :

> a:={1/6,-7/30,31/42,-127/30,2555/66,-1414477/2730,57337/6};
> f:=proc(m) 2^(1-2*m)-1 end;C:=proc(n,p) n!/(p!*(n-p)!) end;
> B:=proc(m) sum('C(2*m,2*l)*a[l]', 'l'=1..(m-1)) end;
> D:=proc(m) f(m)/(f(m)-1)*(1/2-B(m)) end;
> d:=proc(l) D(l)*pi^(2*l)*(-1)^l/f(l)/(2*l)! end;
> d(1);d(2);d(3);d(4);d(5);d(6);d(7);