-
Soit E un K-espace de Banach.
Lc(E) muni de la " norme triple " :
 f
f 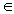 Lc(E),
|||f||| =
Lc(E),
|||f||| = 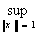 ||f(x)||
||f(x)||
est alors un K-espace de Banach.
- D'après l'étude faite sur les séries entières
d'endomorphismes, comme
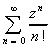 est une série
entière de rayon de convergence infini, si f
est une série
entière de rayon de convergence infini, si f 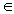 Lc(E), alors on peut définir
Lc(E), alors on peut définir
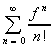 = exp(f) appelée exponentielle
de f.
= exp(f) appelée exponentielle
de f.
Il faut maintenant s'interroger sur la possibilité d'une définition matricielle de l'exponentielle d'un endomorphisme, c'est-à-dire sur l'invariance par changement de base.
- Soit u
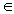 Lc(E).
Soit v
Lc(E).
Soit v 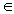 Lc(E)
avec v inversible et v -1
Lc(E)
avec v inversible et v -1
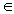 Lc(E).
Lc(E).
On sait alors que pour tout entier n, (v-1uv)n = v-1 un v.
Donc exp(v-1uv) =
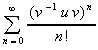 =
= 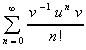 =
= 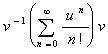 = v-1.exp(u).v
.
= v-1.exp(u).v
.
Soit B une base de E.
Soit A la matrice de u dans B : A = Mat(B, u).
Définissons l'exponentielle de A par
exp(A) = Mat(B, exp(u))
Soit B' une autre base de E.
Soit A' la matrice de u dans B'.
Il existe alors P
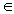 Gln(K)
telle que A' = P-1AP.
Gln(K)
telle que A' = P-1AP.
Soit v l'endomorphisme tel que P = Mat(B, v). On a alors v
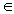 Lc(E)
avec v inversible et v-1
Lc(E)
avec v inversible et v-1
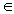 Lc(E).
Lc(E).
Et il vient P-1 = Mat(B, v-1).
exp(A') = Mat(B, exp (v-1 uv)).
La définition de l'exponentielle de matrice est donc légitime et l'on obtientexp(A') = Mat(B, v-1 exp(u) v)
exp(A') = Mat(B, v-1).Mat(B, exp(u)).Mat(B, v)
exp(A') = P-1.Mat(B, exp(u)).P
exp(A') = P-1.exp(A).P
exp(A) =
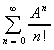
Il vient de cette étude :
-
Soit u
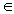 Lc(E).
Lc(E).
Soit v
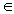 Lc(E),
inversible avec v-1
Lc(E),
inversible avec v-1 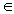 Lc(E).
Lc(E).
Alors :
exp(v-1uv) = v-1.exp(u).v
.
C'est-à-dire matriciellement :
Soient A et A' 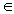 Mn(K).
Mn(K).
Si A et A' sont P-semblables (avec P 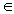 GLn(K)) alors exp(A) et
exp(A') sont aussi P-semblables.
GLn(K)) alors exp(A) et
exp(A') sont aussi P-semblables.
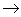
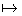 exp(f) est continue.
exp(f) est continue.
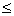 exp(|||f|||)
exp(|||f|||)