Enoncé:
Il n'existe qu'un seul ensemble vide.
Démonstration:
Soient E et F deux ensembles vides. Par définition, on a
 x ,
x
x ,
x E
d'où
E
d'où  x , (x
x , (x E
E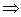 x
x F) (en effet, la proposition P
F) (en effet, la proposition P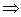 Q est
vraie si P est toujours faux), donc E
Q est
vraie si P est toujours faux), donc E F. Par
symétrie de rôles entre E et F, il vient F
F. Par
symétrie de rôles entre E et F, il vient F E, donc
E=F.
E, donc
E=F.
Enoncé:
Soient E, F, G des ensembles.
On a les propriétés suivantes :
- (E
 G et F
G et F G)
G)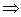 (E
(E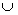 F)
F) G
G
- (G
 E et G
E et G F)
F)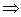 G
G (E
(E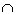 F)
F)
- E
 F
F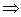 G\F
G\F G\E
G\E
- E
 F
F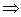 E\G
E\G F\G
F\G
- E=(E
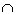 F)
F)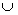 E\F
E\F
Démonstration:
- Soit x
 (E
(E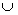 F). Quitte à échanger les
rôles de E et F, on peut supposer x
F). Quitte à échanger les
rôles de E et F, on peut supposer x E.
Alors, comme E
E.
Alors, comme E G, on a x
G, on a x G, CQFD.
G, CQFD.
- Soit x
 G. Par hypothèse, G
G. Par hypothèse, G E et
G
E et
G F, donc x
F, donc x E et x
E et x F, c'est à dire x
F, c'est à dire x E
E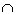 F, CQFD.
F, CQFD.
- Soit x
 G\F. Supposons par l'absurde que x
G\F. Supposons par l'absurde que x G\E;
comme x
G\E;
comme x G\F
G\F G, on aurait alors x
G, on aurait alors x E,
d'où x
E,
d'où x F, ce qui contredit l'hypothèse x
F, ce qui contredit l'hypothèse x G\F.
Donc x
G\F.
Donc x G\E; CQFD.
G\E; CQFD.
- Soit x
 E\G. Alors, d'une part x
E\G. Alors, d'une part x E
E F, donc x
F, donc x F; d'autre part x
F; d'autre part x G;
donc x
G;
donc x F\G, CQFD.
F\G, CQFD.
- Par définition, E\F
 E et E
E et E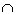 F
F E, donc (E
E, donc (E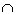 F)
F)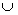 E\F
E\F E.
Réciproquement, soit x
E.
Réciproquement, soit x E; alors ou bien x
E; alors ou bien x F et
x
F et
x (E
(E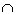 F), ou bien x
F), ou bien x F et
x
F et
x E\F, donc x
E\F, donc x (E
(E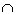 F)
F)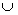 E\F; d'où E
E\F; d'où E (E
(E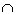 F)
F)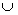 E\F et E=(E
E\F et E=(E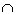 F)
F)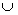 E\F, CQFD.
E\F, CQFD.
Enoncé:
Soient E et F deux ensembles; alors l'ensemble E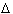 F est
l'ensemble des éléments qui appartiennent à E ou
à F, mais pas aux deux à la fois:
F est
l'ensemble des éléments qui appartiennent à E ou
à F, mais pas aux deux à la fois:
E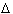 F=(E
F=(E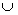 F)\(E
F)\(E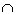 F)
F)
Démonstration:
On a d'une part E (E
(E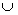 F) donc E\F
F) donc E\F (E
(E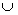 F)\F, d'autre part (E
F)\F, d'autre part (E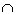 F)
F) F donc
(E
F donc
(E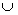 F)\F
F)\F (E
(E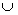 F)\(E
F)\(E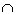 F); d'où E\F
F); d'où E\F (E
(E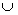 F)\(E
F)\(E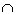 F), de même pour F\E; donc E
F), de même pour F\E; donc E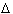 F
F (E
(E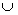 F)\(E
F)\(E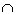 F).
F).
Enoncé:
Soient E, F, G, H quatre ensembles, f une application de E
vers F, g une application de F vers G, h une
application de G vers H. On a
(fog)oh=fo(goh).
Démonstration:
Soit x un élément de E.
On a
((fog)oh)(x)=(fog)(h(x))=f(g(h(x)))=f((goh)(x))=(fo(goh))(x).
Ce résultat est valable pour tout choix de x; il vient
fo(goh)=(fog)oh
Enoncé:
Soient E et F deux ensembles et f une application de E dans
F.
- f est surjective si et seulement s'il existe une
application g de F dans E telle que
fog=IdF. g est alors injective.
- f est injective si et seulement s'il existe une
fonction g de F dans E telle que
gof=IdE. g est alors surjective.
- f est bijective si et seulement s'il existe une
application g de F dans E telle que
fog=IdF et
gof=IdE. g est alors unique; elle
est appelée application inverse (ou réciproque) de
f et notée f-1. g est alors
également bijective, de réciproque f.
Démonstration:
- Supposon d'abord f surjective.
Soit alors y un élément de F; y admet dans E un
antécédent x par f; notons-le g(y).
Alors on a par construction:  y
y F ,
y=f(g(y))=(fog)(y) donc
fog=IdF.
F ,
y=f(g(y))=(fog)(y) donc
fog=IdF.
Réciproquement, si g existe, alors  y
y F ,
y=(fog)(y)=f(g(y))
F ,
y=(fog)(y)=f(g(y))
Tout élément de F admet donc un
antécédent par f, donc f est
surjective.
- Supposons maintenant f injective.
Soit alors y un élément de f(E). y admet dans
x un unique antécédent par f; notons-le
g(y). Alors on a: x
x E ,
(gof)(x)=g(f(x))=x donc
gof=IdE.
E ,
(gof)(x)=g(f(x))=x donc
gof=IdE.
Réciproquement, supposons l'existence de g. Alors si
x et x' sont deux éléments de E tels que
f(x)=f(x'), on a
x=(gof)(x)=g(f(x))=g(f(x'))=(gof)(x')=x'
donc f est injective.
- De plus, il découle des deux critères
précédents que g est injective si et
seulement s'il existe une fonction f de E dans F telle que
fog=IdF et g est injective si et
seulement s'il existe une application f de E dans F telle
que gof=IdE, c'est à dire que
g est injective si et seulement si f est surjective
et g est surjective si et seulement si f est
injective.
- Il découle des deux énoncés
précédents que f est bijective si et
seulement s'il existe une application g de F dans E telle
que fog=IdF et
gof=IdE et que g est alors
également bijective.
Supposons l'existence de g' vérifiant les
mêmes conditions que g. On a alors:
 y
y F ,
F , 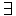 !x
!x E ,
y=f(x) et
g(y)=g(f(x))=(gof)(x)=x=(g'of)(x)=g'(f(x))=g'(y)
E ,
y=f(x) et
g(y)=g(f(x))=(gof)(x)=x=(g'of)(x)=g'(f(x))=g'(y)
c'est-à-dire g=g'; on a donc prouvé
l'unicité de g.
La bijectivité de g se prouve alors par
symétrie des rôles de f et de g.
Enoncé:
Il existe une injection de E dans F si et seulement s'il existe
une surjection de F dans E.
Démonstration:
- Supposons l'existence d'une injection f de E dans F;
alors on a prouvé qu'il existe une surjection g de F
dans E, qui vérifie de plus
gof=IdE.
- De même, s'il existe une surjection g de F dans
E, alors il existe une injection f de E dans F, telle que
fog=IdF.
Enoncé:
#E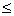 #F
#F #F
#F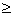 #E
#E
Démonstration:
#E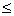 #F
#F Il existe une injection f de E dans F
Il existe une injection f de E dans F Il
existe une surjection g de F dans E
Il
existe une surjection g de F dans E #F
#F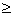 #E
#E
Enoncé:
Soient E et F deux ensembles.
#E=#F (#E
(#E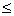 #F et #F
#F et #F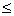 #E)
#E)
Démonstration:
Enoncé:
Soit E un ensemble non vide; alors #E<#P(E).
Démonstration:
- L'application f:E
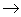 P(E),x
P(E),x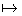 {x}
est injective, donc #E
{x}
est injective, donc #E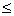 #P(E).
#P(E).
- Supposons maintenant l'existence d'une bijection g de E
sur P(E). Considérons alors le sous-ensemble A de P(E)
défini par: A={x
 E;x
E;x g(x)}. g est
bijective donc A admet un antécédent a. Deux cas se
présentent alors: ou bien a
g(x)}. g est
bijective donc A admet un antécédent a. Deux cas se
présentent alors: ou bien a A,
et alors a
A,
et alors a g(a)=A, ce qui est impossible, ou bien a
g(a)=A, ce qui est impossible, ou bien a A, et
alors a
A, et
alors a g(a)=A, ce qui est également
impossible. On arrive donc à une contradiction, donc
g n'existe pas, donc #E
g(a)=A, ce qui est également
impossible. On arrive donc à une contradiction, donc
g n'existe pas, donc #E #F.
#F.
Enoncé:
Il n'existe pas d'ensemble contenant tous les ensembles.
Démonstration:
Supposons l'existence d'un tel ensemble et notons-le E.
Alors E contient tous les ensembles; en particulier E contient
tous ses sous-ensembles. L'application f:P(E)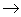 E,X
E,X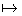 X est
donc définie; elle est évidemment injective donc
#P(E)
X est
donc définie; elle est évidemment injective donc
#P(E)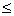 #E, ce qui contredit le théorème de
Cantor.
#E, ce qui contredit le théorème de
Cantor.
Enoncé:
Tout ensemble infini contient un sous-ensemble dénombrable.
Démonstration:
Nous allons construire par récurrence une injection f de
N vers E.
Notons d'abord f(0) un élément quelconque de E.
Considérons l'ensemble E0=E\{f(0)}. L'ensemble E
est infini, donc l'ensemble E0 est non vide. Notons f(1)
un élément quelconque de E0.
Supposons maintenant avoir construit les images des entiers de 1
à n. Notons En=E\{f(1),f(2),...,f(n)}. L'ensemble E
est infini par hypothèse, alors que {f(1),f(2),...,f(n)}est
fini, donc l'ensemble En est non vide; notons f(n+1) un de
ses éléments.
f est ainsi construite par récurrence; elle est injective
par construction, donc l'application g de N dans f(N),
définie par  n
n N , g(n)=f(n), est une bijection de
N sur f(N), qui est donc une partie dénombrable
de E.
N , g(n)=f(n), est une bijection de
N sur f(N), qui est donc une partie dénombrable
de E.
Enoncé:
Un ensemble infini E est dénombrable si et seulement si E
est l'ensemble-image d'une suite.
Démonstration:
- Supposons d'abord E dénombrable. Alors il existe une
bijection f de N sur E. Notons
 n
n N , xn=f(n). Alors
{xn;n
N , xn=f(n). Alors
{xn;n N} est une suite, d'image E car f
est bijective donc surjective.
N} est une suite, d'image E car f
est bijective donc surjective.
- Réciproquement, supposons que E soit l'image d'une
suite {xn;n
 N}.
N}.
La démonstration du théorème
précédent nous donne l'existence d'une injection de
N vers l'ensemble infini E.
D'autre part, notons pour tout élément e de E,
Ne={n;e=xn}, et notons g(e) un
élément quelconque de Ne. L'application g
de E vers N ainsi définie est injective par
construction (en effet, si g(e)=g(e')=n, alors
e=e'=xn).
Il existe donc une injection f de N vers E et une injection
g de E vers N; le théorème de
Cantor-Bernstein nous dit que E et N sont alors en
bijection, c'est à dire que E est dénombrable, CQFD.
Enoncé:
Soit (E,+) un magma. S'il existe dans E un élément
neutre pour la loi +, alors cet élément est unique.
Démonstration:
Soient e et e' deux éléments neutres.
e est élément neutre donc e+e'=e'.
e' est élément neutre donc e+e'=e.
Donc e=e'.
Enoncé:
Soit (E,+) un magma dont la loi admet un élément
neutre 0; soit x un élément de E.
Si x est inversible pour la loi +, et si la loi + est associative,
alors l'inverse de x est défini de façon unique.
Démonstration:
Supposons x inversible et notons y et z deux inverses de x. La loi
+ étant associative et 0 étant élément
neutre, on a:
z=0+z=(y+x)+z=y+(x+z)=y+0=y
Enoncé:
Soit (E,+) un magma dont la loi + est associative et admet un
élément neutre 0. Alors tout élément
inversible à droite (resp. à gauche) de E est
régulier à droite (resp. à gauche).
Démonstration:
- Soit x un élément de E inversible à
droite et y un inverse à droite de x; soient u et v deux
éléments quelconques de E. On a:
u+x=v+x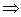 (u+x)+y=(v+x)+y
(u+x)+y=(v+x)+y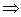 u+(x+y)=v+(x+y)
u+(x+y)=v+(x+y)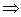 u+0=v+0
u+0=v+0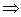 u=v
u=v
- Soit x un élément de E inversible à
gauche et z un inverse à gauche de x; soient u et v deux
éléments quelconques de E. On a:
x+u=x+v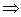 z+(x+u)=z+(x+v)
z+(x+u)=z+(x+v)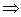 (z+x)+u=(z+x)+v
(z+x)+u=(z+x)+v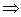 0+u=0+v
0+u=0+v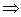 u=v
u=v
Enoncé:
Soit (E,~) un ensemble muni d'une relation d'équivalence.
L'ensemble des classes d'équivalence forme une partition de
l'ensemble E.
Démonstration:
 x
x E , x~x donc x
E , x~x donc x cl(x): les classes d'équivalence sont toutes
non vides et tout élément de E appartient à
une classe d'équivalence.
cl(x): les classes d'équivalence sont toutes
non vides et tout élément de E appartient à
une classe d'équivalence.
- Supposons que deux classes d'équivalence cl(x) et cl(y)
ne soient pas disjointes. Alors
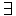 z
z cl(x)
cl(x)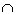 cl(y). C'est à dire que par
définition des classes x~z et y~z. La relation ~
étant transitive, il vient
cl(y). C'est à dire que par
définition des classes x~z et y~z. La relation ~
étant transitive, il vient  t
t cl(x) , t~x donc t~z et t~y, d'où t
cl(x) , t~x donc t~z et t~y, d'où t cl(y) et cl(x)
cl(y) et cl(x) cl(y); par symétrie de
rôles entre x et y, on a également cl(y)
cl(y); par symétrie de
rôles entre x et y, on a également cl(y) cl(x), d'où cl(y)=cl(x), CQFD.
cl(x), d'où cl(y)=cl(x), CQFD.
Enoncé:
Considérons la relation binaire R sur E définie par
 (x,y)
(x,y) E2 , xRy
E2 , xRy f(x)=f(y). C'est une relation
d'équivalence.
f(x)=f(y). C'est une relation
d'équivalence.
Démonstration:
 x
x E , f(x)=f(x) donc xRx; R est
réflexive.
E , f(x)=f(x) donc xRx; R est
réflexive.
 (x,y)
(x,y) E2 ,
(f(x)=f(y)
E2 ,
(f(x)=f(y) f(y)=f(x)) c'est à
dire (xRy
f(y)=f(x)) c'est à
dire (xRy yRx); R est symétrique.
yRx); R est symétrique.
- Soient x, y, z trois éléments de E avec xRy et
yRz. C'est à dire f(x)=f(y) et
f(y)=f(z), d'où f(x)=f(z) et
xRz; R est transitive.
Enoncé:
L'application s:E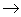 E/R,x
E/R,x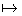 cl(x) est surjective.
cl(x) est surjective.
Démonstration:
Soit y E/R. Par définition
E/R. Par définition 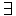 x
x E ,
y=cl(x), c'est à dire y=s(x).
E ,
y=cl(x), c'est à dire y=s(x).
Enoncé:
L'application b:E/R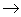 f(E),y=cl(x)
f(E),y=cl(x)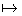 b(y)=f(x) est définie (c'est
à dire qu'elle ne dépend pas du choix de x comme
représentant de y); elle est de plus bijective.
b(y)=f(x) est définie (c'est
à dire qu'elle ne dépend pas du choix de x comme
représentant de y); elle est de plus bijective.
Démonstration:
- Par définition de R, si on se donne x et x' tels que
cl(x)=cl(x'), alors f(x)=f(x'), donc l'application
b est bien définie.
- Soient y=cl(x) et y'=cl(x') deux éléments de E/R
tels que b(y)=b(y'). Alors f(x)=f(x')
par définition de b, c'est à dire xRx' et
donc y=cl(x)=cl(x')=y'; b est injective.
- Soit z
 f(E). Alors
f(E). Alors 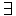 x
x E ,
z=f(x) et par définition de b,
z=b(cl(x)); b est surjective.
E ,
z=f(x) et par définition de b,
z=b(cl(x)); b est surjective.
Enoncé:
f=iobos
Démonstration:
Soit x un élément quelconque de E.
Par définition de b et de s, on a:
f(x)=b(cl(x))=b(s(x))=(bos)(x).
De plus, f(x) f(E) donc
f(x)=i(f(x))=i((bos)(x))=(iobos)(x).
f(E) donc
f(x)=i(f(x))=i((bos)(x))=(iobos)(x).
Ce résultat est indépendant de x, donc
f=iobos.
![]() x ,
x
x ,
x![]() E
d'où
E
d'où ![]() x , (x
x , (x![]() E
E![]() x
x![]() F) (en effet, la proposition P
F) (en effet, la proposition P![]() Q est
vraie si P est toujours faux), donc E
Q est
vraie si P est toujours faux), donc E![]() F. Par
symétrie de rôles entre E et F, il vient F
F. Par
symétrie de rôles entre E et F, il vient F![]() E, donc
E=F.
E, donc
E=F.
![]() F est
l'ensemble des éléments qui appartiennent à E ou
à F, mais pas aux deux à la fois:
F est
l'ensemble des éléments qui appartiennent à E ou
à F, mais pas aux deux à la fois:![]() F=(E
F=(E![]() F)\(E
F)\(E![]() F)
F)
![]() (E
(E![]() F) donc E\F
F) donc E\F![]() (E
(E![]() F)\F, d'autre part (E
F)\F, d'autre part (E![]() F)
F)![]() F donc
(E
F donc
(E![]() F)\F
F)\F![]() (E
(E![]() F)\(E
F)\(E![]() F); d'où E\F
F); d'où E\F![]() (E
(E![]() F)\(E
F)\(E![]() F), de même pour F\E; donc E
F), de même pour F\E; donc E![]() F
F![]() (E
(E![]() F)\(E
F)\(E![]() F).
F).
![]() #F
#F![]() #F
#F![]() #E
#E
![]() #F
#F![]() Il existe une injection f de E dans F
Il existe une injection f de E dans F![]() Il
existe une surjection g de F dans E
Il
existe une surjection g de F dans E![]() #F
#F![]() #E
#E
![]() (#E
(#E![]() #F et #F
#F et #F![]() #E)
#E)
![]() E,X
E,X![]() X est
donc définie; elle est évidemment injective donc
#P(E)
X est
donc définie; elle est évidemment injective donc
#P(E)![]() #E, ce qui contredit le théorème de
Cantor.
#E, ce qui contredit le théorème de
Cantor.
![]() n
n![]() N , g(n)=f(n), est une bijection de
N sur f(N), qui est donc une partie dénombrable
de E.
N , g(n)=f(n), est une bijection de
N sur f(N), qui est donc une partie dénombrable
de E.
![]() (x,y)
(x,y)![]() E2 , xRy
E2 , xRy![]() f(x)=f(y). C'est une relation
d'équivalence.
f(x)=f(y). C'est une relation
d'équivalence.
![]() E/R,x
E/R,x![]() cl(x) est surjective.
cl(x) est surjective.
![]() E/R. Par définition
E/R. Par définition ![]() x
x![]() E ,
y=cl(x), c'est à dire y=s(x).
E ,
y=cl(x), c'est à dire y=s(x).
![]() f(E),y=cl(x)
f(E),y=cl(x)![]() b(y)=f(x) est définie (c'est
à dire qu'elle ne dépend pas du choix de x comme
représentant de y); elle est de plus bijective.
b(y)=f(x) est définie (c'est
à dire qu'elle ne dépend pas du choix de x comme
représentant de y); elle est de plus bijective.
![]() f(E) donc
f(x)=i(f(x))=i((bos)(x))=(iobos)(x).
f(E) donc
f(x)=i(f(x))=i((bos)(x))=(iobos)(x).