Comme chaque nombre premier intervenant dans la décomposition de 30 a une valuation de 1, il suffit de montrer que chaque nombre premier divise n5 - n, pour que leur produit qui est alors 30, le divise.
On a n5 - n = n.(n4 - 1)
Si n est pair, on a 2 | n, donc 2 | n.(n4 - 1) d'où 2 | n5 - n.
Sinon, n est impair et alors n4 aussi donc n4 - 1 est pair.
Il vient donc 2 | n4
- 1, soit 2 | n5
- n.
Finalement, dans tous les cas 2
| n5
- n
On a n5 - n = n.(n4 - 1) = n.(n² - 1).(n² + 1) = (n3 - n).(n² + 1)
3 étant un nombre premier, alors, d'après le petit théorème de Fermat
 n
n 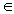 N, n3
N, n3
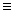 n [3]
n [3]
Soit 3 | n3 - n et alors 3 | n5 - n
- Remarque :
On pouvait s'en sortir sans employer le petit théorème de Fermat, en considérant simplement les classes modulo 3 de n, et s'apercevoir que 3 divisait alors obligatoirement n ou n2 - 1 (donc n3 - n ).En effet :
Soit n
0 [3] donc 3 | n.
Soit n1 [3] donc n²
1 [3] et 3 | n² - 1
Soit n2 [3] donc n²
1 [3] et 3 | n² - 1
5 étant un nombre premier, alors, d'après le petit théorème de Fermat,
 n
n 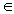 N, n5
N, n5 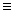 n [5]
n [5]
D'où 5 | n5 - n
(Cette fois-ci, l'étude des différentes classes modulo 5 devient plus fastidieuse...)
D'où 30 | n5 - n