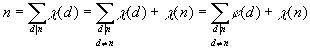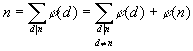- Enoncé

f(1) = 1.
Si p est un nombre premier alors f(p) = p-1.
Si p est un nombre premier et a un entier naturel, alors f(p^a) = p^a-1.(p-1).
Soit n et m deux entiers naturels premiers entre eux. Il vient f(m.n) = f(m).f(n).

- Démonstration

• Z/1Z = {0}, donc il n’a qu’un seul générateur, 0.
D’où f(1) = 1.

• Soit p un nombre premier.
1, 2, ..., p-1 sont premiers avec p et n’ont pas la même classe dans Z/pZ (et il est clair qu’il n’y a pas d’autres entiers premiers avec p qui aient une classe différente). D’où f(p) = p-1.

• Soit p un nombre premier.
Soit a un entier naturel.
Calculer f(p^a) revient à compter le nombre d’entiers compris entre 1 et p^a (inclus) qui sont premiers avec p^a. Comme p est premier, cela revient à dénombrer le nombre d’entiers de 1..p^a qui ne sont pas divisibles par p, c’est-à-dire tous les entiers sauf les multiples de p.
Comme il y a p^a-1 multiples de p, il vient : f(p^a) = p^a - p^a-1 = p^a-1.(p-1).

• Soit n et m deux entiers naturels tels que n /\ m = 1.
D’après le théorème chinois, on sait que Z/mnZ est en bijection avec Z/nZ x Z/mZ par une application q qui à un élément de Z/mnZ associe un couple composé de sa classe dans Z/nZ et de sa classe dans Z/mZ.
On va montrer que q induit une bijection entre les éléments de Z/mnZ qui sont premiers avec mn et les couples (a, b) de Z/nZ x Z/mZ où a est premier avec n et b premier avec m.
Soit u de Z/mnZ, premier avec mn.
D’après le théorème de Bezout, il existe r et s deux entiers tels que r.u + s.mn = 1, d’où l’on déduit immédiatement que u est premier avec m et aussi avec n (toujours gràce au théorème de Bezout).
Soit maintenant (a, b) un couple de Z/nZ x Z/mZ tel que a /\ n = 1 et b /\ m = 1.
On prend y de Z/mnZ tel que q(y) = (a, b). Cet élément existe car q est une bijection et de plus, il est différent pour tout couple (a, b) choisi.
D’après le théorème de Bezout, il existe des entiers r₁, s₁, r₂ et s₂ tels que :
a.r₁ + n.s₁ = 1
b.r₂ + m.s₂ = 1
D’autre part a = y + k₁.n et b = y + k₂.m, d’où
(y + k₁.n).r₁ + n.s₁ = 1
(y + k₂.m).r₂ + m.s₂ = 1
Ce qui peut s’écrire, en posant u = k₁.r₁ + s₁ et v = k₂.r₂ + s₂,
y.r₁ + n.u = 1
y.r₂ + m.v = 1
Soit, en faisant le produit,
y.(r₁.r₂.y + r₁.m.v + r₂.n.u) + nm.uv = 1
Ce qui prouve bien (théorème de Bezout), que y est premier avec mn.
On a donc une bijection entre les éléments inversibles de Z/mnZ et ceux de Z/nZ x Z/mZ.
Comme ce sont des ensembles finis, leurs cardinaux sont égaux.
D’où f(mn) = f(n).f(m)

- Enoncé

Soit n un entier naturel.
Alors, il vient :

- Démonstration

Le résultat est évident pour n = 1 (car f(1) = 1).
Supposons le vrai jusqu’à n-1.
Si n est premier, ses seuls diviseurs positifs sont 1 et n.
Or f(1) = 1 et f(n) = n-1 car n est premier.
Donc
Sinon, il peut se décomposer en produit de deux entiers naturels u et v différents de 1 et premiers entre eux.
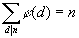
On a alors . Comme u et v sont premiers entre eux, d peut se décomposer sous la forme d₁.d₂ avec d₁|u et d₂|v.
D’où.
Or u et v étant premiers entre eux, d₁ et d₂ sont aussi premiers entre eux. D’après la proposition II.1, il vient f(d₁.d₂) = f(d₁).f(d₂).
Donc : .
D’après l’hypothèse de récurrence, il vient et .
D’où
Par récurrence, le résultat est bien démontré.

- Enoncé

Soit c, une fonction de N^* dans N.
Si, pour tout entier naturel n non nul, on a , alors f = c.

- Démonstration

Pour le cas n = 1, le résultat est évident.
Supposons le résultat vrai pour tout m < n.
On a alors :

Or, d’après la proposition II.2, on a

D’où c(n) = f(n).
Il vient donc par récurrence que c = f.