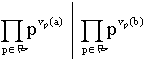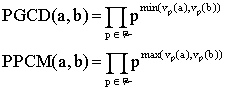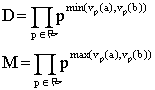Démonstrations du cours de divisibilité

- Enoncé :

(a, b) Z² ( a|b b aZ )

- Démonstration :

Soient a et b deux entiers relatifs.

a|b c Z / a.c = b b aZ

- Autre formulation :

a|b c Z / a.c = b b 0 [a]

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les congruences
Ouvrir le cours sur les symboles logiques

- Enoncé

Soient a et b deux entiers relatifs.

a|b bZ aZ

- Démonstration

Soient a et b deux entiers relatifs.

Montrons que a|b bZ aZ

Soit x bZ

u Z / x = b.u

Or a|b donc c Z / b = a.c

On a donc x = b.u = (a.c).u = a.(c.u)

Finalement x aZ

Soit bZ aZ

Montrons que bZ aZ a|b

On a b aZ, donc

c Z / b = a.c

D'où a|b

L'équivalence est donc démontrée.

Ouvrir cours sur la divisibilité
Ouvrir cours sur les sous-groupes de Z

- Enoncé

Soient a,b et m des entiers relatifs.

Si a|b alors a|b.m

- Démonstration

Soient a,b et m deux entiers relatifs.

Si a|b alors, d'après la proposition I.2, bZ aZ

Or b.m bZ donc, b.m aZ

D'après la proposition I.1, on a alors a|b.m

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z.

- Enoncé

Soient a, b et c trois entiers relatifs.

Si a | b et a | c alors a | (b+c)

- Démonstration

Soient a, b et c trois entiers relatifs.

Si a | b et a | c alors il existe deux entiers relatifs u et v tels que

a.u = b et a.v = c

Alors b + c = a.u + a.v = a.(u + v) donc a | (b+c)

- Remarque

Une simple récurrence généralise à une somme de n entiers :

Soit a un entier relatif.

Soit (b_i)_{i N} une famille presque nulle d'entiers relatifs.

Si, pour tout i N, a | b_i, alors a | ()

On déduit alors facilement de la proposition I.3

Il vient donc :

Soient (b_i)_{i N} ,(m_i)_{i N} deux familles presque nulles d'entiers relatifs.

Si, pour tout i N, a | b_i, alors a | ()

Ouvrir le cours sur la divisibilité

- Etude de la réciproque

Le but est de montrer qu'à part les cas triviaux, si un entier relatif “ a ” donné divise un autre entier relatif “ n ”, il ne divise en aucun cas un élément de tout couple d'entiers relatifs dont la somme serait “ n ”.

Soient deux entiers relatifs a et d tels que a | d

Soient deux entiers relatifs b et c tels que b + c = d

Remarquons tout d'abord que si a | b alors a | c car, d'après la proposition I.4,

a | ( d + (-b) )

Supposons a +1 et a -1 auquel cas la réciproque est évidente.

On peut écrire d = 1 + (d-1) donc, si la réciproque était vérifiée, on aurait a | 1

ce qui est impossible car a 1 et a -1, qui sont les seuls diviseurs de 1 dans Z.

( Voir démonstration )

Si on étudie la réciproque en la restreignant aux couples d'entiers naturels dont la somme vaut “ n ”, les cas où n = 0 et n = 1 s'ajoutent aux cas précédents mais cela n'apporte rien d'intéressant de plus.

Ouvrir cours sur la divisibilité

- Réflexivité

Soit m un entier relatif.

Z étant un anneau on a m = 1.m

D'où m | m

- Transitivité

Soient m, n et p trois entiers relatifs.

Si m | n et n | p alors, par définition, il existe deux entiers relatifs u et v tels que :

n = m.u et p = n.v

Donc p = n.v = (m.u).v = m.(u.v)

D'où m | p

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les relations binaires

- Enoncé

Soient a et b deux entiers relatifs.

On note aZ + bZ l'ensemble {a.u + b.v ; (u,v) Z²}

aZ + bZ est un idéal, contenant a et b

- Démonstration

Soient a et b deux entiers relatifs.

aZ + bZ = {a.u + b.v ; (u,v) Z²}

En prenant u = 1 et v = 0 (et vice-versa), on voit que a et b appartiennent à aZ + bZ

Montrons que aZ + bZ est un sous-groupe additif de Z.

Soient x et y deux éléments de aZ + bZ.

Il existe alors quatre entiers relatifs i, j, k et l tels que

x = a.i + b.j et y = a.k + b.l

On a alors x - y = a.(i-k) + b.(j-l) donc x - y aZ + bZ

Comme l'ensemble n'est pas vide, c'est un sous-groupe de Z.

Soit n un entier relatif.

Soit x un élément de aZ + bZ.

Il existe alors deux entiers relatifs i et j tels que :

x = a.i + b.j

On a n.x = x.n = a.(n.i) + b.(n.j)

aZ + bZ est donc un idéal bilatère.

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les anneaux

- Enoncé

Soient a et b deux entiers relatifs.

Un PGCD de (a,b) est unique au signe près.

- Démonstration

Soient a et b deux entiers relatifs.

Soit d un PGCD de (a,b).

Soit d' un autre PGCD de (a,b).

On a d'Z = dZ.

L'étude des sous-groupes de Z nous a montré qu'alors

d = +d' ou d = -d'.

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

- Enoncé

Soient a et b deux entiers relatifs.

Soit d = PGCD(a,b)

Il existe alors deux entiers relatifs u et v tels que d = a.u + b.v

- Démonstration

Soient a et b deux entiers relatifs.

Soit d = PGCD(a,b)

Par définition dZ = aZ + bZ = { a.j + b.k ; (j,k) Z² }

Donc d { a.j + b.k ; (j,k) Z² } soit :

Il existe deux entiers relatifs u et v tels que d = a.u + b.v

Ouvrir le cours sur la divisibilité

- Enoncé

Soient a, b et v trois entiers relatifs.

On a alors PGCD(v.a, v.b) = |v|.PGCD(a,b)

- Démonstration

Soient a, b et v trois entiers relatifs.

Soient d = PGCD(a,b) et D = PGCD(v.a, v.b)

Le but est donc de montrer que (|v|.d)Z = DZ

On démontrera tout d'abord que (|v|.d)Z DZ puis que DZ (|v|.d)Z

D'après l'identité de Bezout, il existe deux entiers relatifs q et p tels que

a.q + b.p = d

En multipliant par v, il vient

(v.a).q + (v.b).p = v.d

Quitte à changer q en -q et p en -p si v est négatif, on a

|v|.d = (v.a).q + (v.b).p

donc (|v|.d)Z (v.a)Z + (v.b)Z = DZ

Soit m DZ

D'après la définition de (v.a)Z + (v.b)Z il existe alors deux entiers relatifs f et g tels que

m = (v.a).f + (v.b).g

Comme précédemment, quitte à changer le signe de f et g si v est négatif, on a

m = (|v|.a).f + (|v|.b).g = |v|.(a.f + b.g)

Comme a.f + b.g appartient à dZ, alors |v|.(a.f + b.g) appartient à |v|.dZ

D'où m dZ et DZ dZ

Finalement DZ = dZ soit PGCD(v.a, v.b) = |v|.PGCD(a, b)

Remarque :

On peut éviter dans cette démonstration l'emploi des valeurs absolue (ce qui supprime l'emploi désagréable de l'expression " Quitte à changer ... "); pour cela il suffit d'employer la même méthode mais pour démontrer que (v.d)Z = DZ, et ensuite conclure en se basant sur le caractère positif que doit avoir le PGCD d'un couple d'entiers relatifs.

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

-Enoncé

Soient a et b deux entiers relatifs.

PGCD(a, b) = PGCD(|a|, |b|)

-Démonstration

Soient a et b deux entiers relatifs.

Posons d = PGCD(a, b) et D = PGCD(|a|, |b|)

L'étude des sous-groupes de Z nous donne

aZ = |a|Z et bZ = |b|Z

On a alors dZ = aZ + bZ = |a|Z + |b|Z = DZ

Comme d et D sont de même signe et qu'ils engendrent le même sous-groupe de Z, on a déjà montré que D = d.

D'où

PGCD(a, b) = PGCD(|a|, |b|)

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

- Enoncé

Soient a et b deux entiers relatifs.

(a, b) (0, 0) PGCD(a, b) 0

- Démonstration

Soient a et b deux entiers relatifs.

Si PGCD(a, b) = 0, alors aZ + bZ = 0Z = {0}

Donc aZ {0} et bZ {0}

On a alors

( aZ = ou aZ = {0} ) et ( bZ = ou bZ = {0} )

Comme aZ et bZ ne peuvent être vides, on a alors obligatoirement :

aZ = bZ = {0}

D'après l'étude menée sur les sous-groupes de Z, il vient donc a = b = 0

Soit (a, b) = (0, 0)

D'autre part, notre étude des PGCD particuliers, nous a montré que PGCD(0, 0) = 0

On a donc montré l'équivalence suivante :

(a, b) = (0, 0) PGCD(a, b) = 0

Le passage à la contre-apposée, il vient

(a, b) (0, 0) PGCD(a, b) 0

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

- Enoncé

Soient a et b deux entiers relatifs.

S'il existe deux entiers relatifs q et r tels que a = b.q + r alors

PGCD(a, b) = PGCD(b,r)

- Démonstration

Soient a et b deux entiers relatifs.

Par hypothèse, il existe q et r deux entiers relatifs tels que a = b.q + r

Posons d = PGCD(a, b) et d' = PGCD(b, r)

On a d|b, donc d|b.q (Proposition I.4)

Comme d|a et d|b.q alors d|(a-b.q) donc d|r

Finalement, d est un diviseur commun à b et à r, il divise donc d' d'après la caractérisation du PGCD.

On a d'|b, donc d'|b.q (Proposition I.4)

Comme d'|r et d'|b.q alors d|(b.q + r) donc d'|a

Finalement, d' est un diviseur commun à a et à b, il divise donc d d'après la caractérisation du PGCD.

Nous avons donc démontré que

d | d' et d' | d

Comme d et d' sont positifs, l'étude de l'antisymétrie de la relation de divisibilité nous donne d = d'

D'où :

PGCD(a, b) = PGCD(b, r)

Ouvrir le cours sur la divisibilité

-Enoncé

Soient a et b deux entiers relatifs non tous nuls.

Alors sont premiers entre eux.

-Démonstration

Soient a et b deux entiers relatifs non tous nuls.

D'après la proposition II.3, on sait que PGCD(a, b) est non nul et l'on peut donc diviser par PGCD(a, b).

D'autre part, la caractérisation du PGCD nous indique que PGCD(a, b) divise a et b, d'où sont des entiers relatifs.

Si n'étaient pas premiers entre eux, il existerait un entier naturel n strictement supérieur à 1 tel que n divise , donc n.PGCD(a, b) divise a et b.

Comme n est strictement supérieur à 1, n.PGCD(a, b) est un diviseur commun à a et à b plus grand que le PGCD(a, b), ce qui est absurde d'après la caractérisation du PGCD.

D'où :

sont premiers entre eux.

Ouvrir le cours sur la divisibilité

-Enoncé

Soit p un entier naturel.

p est premier ssi il admet exactement deux diviseurs positifs.

-Démonstration

Soit p un entier naturel.

Soit a un entier relatif.

Si a | p alors c Z / a.c = p donc (-a).(-c) = p et -a divise p

D'après ce qu'on vient de dire, si on partitionne l'ensemble des diviseurs de p en trois parties :

1- Ceux qui sont strictement positifs

2- Ceux qui sont nuls

3- Ceux qui sont strictement négatifs

on s'aperçoit alors qu'il y a autant d'éléments dans " 1 " que dans " 3 ".

D'autre part si 0 est diviseur, alors p est nul et admet alors une infinité de diviseurs.

Donc :

p admet exactement quatre diviseurs p admet exactement deux diviseurs positifs

Comme p est premier p admet exactement deux diviseurs positifs

il vient

p est premier p admet exactement deux diviseurs positifs

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur les nombres premiers

-Enoncé

Soit p un entier naturel.

p est premier ssi p n'est divisible que par 1,-1,p et -p

ssi les seuls diviseurs positifs de p sont 1 et lui-même (soit p)

-Démonstration

La démonstration de la C.N.S. 1 permet de démontrer l'équivalence entre la C.N.S. 2 et la C.N.S. 2 bis.

Nous démontrerons le résultat en montrant l'équivalence de la C.N.S. 1 avec la

C.N.S. 2 bis.

Soit p un entier naturel.

On a p = p.1 donc 1 et p divisent p et sont positifs.

Or p est premier p admet exactement deux diviseurs positifs

Comme p et 1 divisent p et sont positifs, on a :

p n'admet que deux diviseurs positifs p n'admet que p et 1 comme diviseurs positifs

Comme p et 1 sont positifs

p n'admet que p et 1 comme diviseurs positifs p n'admet que deux diviseurs positifs

D'où

p est premier p n'admet que p et 1 comme diviseurs positifs

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur les nombres premiers

-Enoncé

Il n'y a qu'un nombre premier pair

-Démonstration

On a vu que 2 était premier et pair.

Soit n un entier pair positif différent de 2.

Par définition des entiers pairs, 2|n

Or 2 n et 2 1, donc n admet plus de deux diviseurs positifs.

D'après la C.N.S. 2 bis, n ne peut pas être premier.

Il n'y a donc qu'un seul nombre premier pair.

Ouvrir le cour sur la divisibilité
Ouvrir l'article sur les nombres premiers

---

Proposition II.4

-Enoncé

Soit p un nombre premier et m un entier relatif.

PGCD(p,m) = 1 m pZ

-Démonstration

Soit p un nombre premier.

Soit m un entier relatif.

Posons d = PGCD(p, m)

On a, par caractérisation du PGCD, d|p et d|m

Comme d|p alors, d'après la C.N.S.2 bis, d = 1 ou d = p

Si m pZ, alors p|m.

Donc p|d, car d est le plus grand des diviseurs communs à p et m.

Finalement d = p et PGCD(p, m) 1

Si m pZ alors, comme d|m, d p (sinon on aurait p|m et m pZ )

Donc d = 1, soit PGCD(p, m) = 1

D'où :

PGCD(p, m) = 1 m pZ

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur les nombres premiers

---

Théorème de Bezout

-Enoncé

Soient a et b deux entiers relatifs.

PGCD(a,b) = 1 (u,v) Z² / a.u + b.v = 1

-Démonstration

Soient a et b deux entiers relatifs.

Supposons que PGCD(a, b) = 1

D'après l'identité de Bezout, il existe u et v deux entiers relatifs tels que

a.u + b.v = 1

Supposons qu'il existe u et v deux entiers relatifs tels que

a.u + b.v = 1

Posons d = PGCD(a, b)

On a d|a et d|b donc d|a.u et d|b.v d'où d|(a.u + b.v) soit d|1

Comme d est positif, d = 1

PGCD(a, b) = 1

Il vient donc

PGCD(a, b) = 1 (u, v) Z² / a.u + b.v = 1

Ouvrir le cours sur la divisibilité

---

Théorème de Gauss

-Enoncé

Soient a, b et c trois entiers relatifs.

Si a | b.c et si a est premier avec b alors a | c

-Démonstration

Soient a, b et c trois entiers relatifs.

Si PGCD(a, b) = 1, alors, d'après le théorème de Bezout, il existe u et v deux entiers relatifs tels que a.u + b.v = 1

Donc, en multipliant tout par c,

a.(c.u) + (b.c).v = c

Comme a | a alors a | a.(c.u)

Comme, par hypothèse, a | b.c, a | (b.c).v

Donc a | ( a.(c.u) + (b.c).v )

D'où a | c

- Remarque

Seule l'identité de Bezout suffisait.

Ouvrir le cours sur la divisibilité

---

Théorème d'Euclide

-Enoncé

Soient a et b deux entiers relatifs et p un nombre premier.

Si p divise a.b alors p divise a ou p divise b.

-Démonstration

Soient a et b deux entiers relatifs.

Soit p un nombre premier.

Si p | a alors le résultat est démontré.

Sinon, p ne divise pas a, c'est-à-dire que (Proposition I.1) a pZ

D'après la proposition II.4, on a alors PGCD(p, a) = 1.

Comme p | a.b et que p est premier avec a alors, d'après le théorème de Gauss,

on a p | b.

Finalement p|a ou p|b.

- Remarque

Le théorème se généralise facilement à un produit de n facteurs.

Soient a1,a2,..an n entiers relatifs.

Soit p un nombre premier.

Si p | a1.a2...an alors p | (a1.a2..an-1).an

Donc, d'après le théorème que l'on vient de démontrer, p | an ou p | a1.a2...an-1

Quitte à réitérer le même processus n-1 fois, on montre ainsi qu'il existe i n tel que p | ai

Ouvrir le cours sur la divisibilité

Ouvrir l'article sur les nombres premiers

---

Proposition III.1

-Enoncé

Un PPCM d'un couple d'entiers relatifs est unique au signe près.

-Démonstration

Soient a et b deux entiers relatifs.

Soit m et m', deux PPCM de (a, b).

On a mZ = aZ bZ = m'Z, soit mZ = m'Z

L'étude des sous-groupes de Z nous a montré qu'alors

m = +m' ou m = -m'.

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

---

Proposition III.2

-Enoncé

Soient a, b et l des entiers relatifs.

PPCM(l.a, l.b) = |l|.PPCM(a,b)

-Démonstration

Soient a, b et l des entiers relatifs.

Posons m = PPCM(a, b) et L = PPCM(l.a, l.b).

Il nous faut montrer que (l.m)Z = LZ.

LZ = (l.a)Z (l.b)Z = { x Z ; (u,v) Z² / x = (l.a).u = (l.b).v }

mZ = { x Z ; (u,v) Z² / x = a.u = b.v }

D'après l'étude des sous-groupes de Z, il vient

(l.m)Z = l.(mZ) = { l.x Z ; x mZ } = { y Z ; y = l.(a.u) = l.(b.v) } = LZ

La même étude nous a aussi montré que (-l.m)Z = (l.m)Z donc (l.m)Z = (|l|.m)Z

D'où :

PPCM(l.a, l.b) = |l|.PPCM(a,b)

-Remarque

Comme pour le PGCD, on a PPCM(a, b) = PPCM(|a|, |b|)

En effet aZ = |a|Z et bZ = |b|Z donc aZ bZ = |a|Z |b|Z

Il vient alors PPCM(a, b)Z = PPCM(|a|, |b|)Z, et comme ils ont le même signe

PPCM(a, b) = PPCM(|a|, |b|)

Ouvrir le cours sur la divisibilité
Ouvrir le cours sur les sous-groupes de Z

---

Théorème fondamental de l'arithmétique

-Enoncé

Tout entier strictement supérieur à 1 se décompose de façon unique en produit de facteurs premiers.

-Démonstration

Nous allons démontrer ce résultat par récurrence.

Le résultat est évidemment vrai pour n = 2.

Supposons que le résultat soit vrai pour tous les entiers inférieurs ou égaux à n.

Considérons l'entier n+1.

Si n+1 est premier, alors il se décompose en produit d'un seul nombre premier, lui- même. L'étude faite des nombres premiers donne alors l'unicité.

Sinon, n+1 n'étant pas premier, il vient

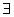(c,d) 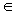Z² / n+1 = c.d

On a alors

c 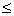n et d 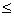n

D'après l'hypothèse de récurrence, c et d admettent une décomposition en produit de facteurs premiers, il en est donc de même pour leur produit.

Il reste à montrer que les facteurs sont uniques (à l'ordre près ).

Supposons qu'il existe deux décompositions en produit de nombres premiers, on a alors

n+1 = p1.p2....pr = m1.m2....ms

avec

i {1,..r} pi est premier

k {1,..t} mk est premier.

Il vient alors que p1 | n+1 donc p1 | m1.m2....ms

D'après le théorème d'Euclide (voir la remarque), i {1,..s} tel que p1 | mi

On a alors obligatoirement p1 = mi (découle directement de la notion de nombre premier).

En renumérotant m1, m2,..mt, de telle manière que p1 = m1, on obtient

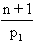= p2..pr = m2..mt et par hypothèse de récurrence, car 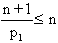, on a l'unicité de la décomposition de donc

r = t

et i {1,..r}, pi = mi.

La décomposition de n+1 est donc unique.

Le cas n+1 est donc vrai; on démontre ainsi par récurrence le résultat voulu.

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur la récurrence

---

Proposition V.1

-Enoncé

Soient a et b deux entiers naturels non nuls

a|b p P, vp(a) vp(b)

-Démonstration

Soient a et b deux entiers naturels non nuls

D'après ce qu'il vient d'être démontré, on peut écrire

et

Si a | b alors, p P, .

Soit p un nombre premier fixé.

D'après le théorème de Gauss, comme p est premier avec tous les autres nombres premier sauf lui-même, .

Si p P, vp(a) vp(b)

On a alors p P , et il vient

soit a | b.

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur les nombres p-adiques
Consulter les notations

---

Proposition V.2

-Enoncé

Soient a et b deux entiers naturels non nuls.

On a alors

-Démonstration

Soient a et b deux entiers naturels non nuls.

Posons d = PGCD(a, b) et m = PPCM(a, b).

Posons

D'après la proposition V.1, on constate que D est un diviseur commun à a et à b et M est un multiple commun à a et b.

On a donc D | d

Supposons que D d, alors il existe p P tel que p | , soit p tel que

.

Quitte à inverser a et b, on peut supposer que min(vp(a), vp(b)) = vp(a)

Comme d | a, il vient

ce qui est absurde de par l'unicité de la décomposition en produit de facteurs premiers.

Finalement D = d = PGCD(a, b)

Nous allons maintenant démontrer que M = m de manière analogue à la démonstration précédente.

On a donc m | M

Supposons que m M, alors il existe p P tel que p | , soit p tel que

.

Quitte à inverser a et b, on peut supposer que max(vp(a), vp(b)) = vp(a)

Comme a | m, il vient

ce qui est absurde de par l'unicité de la décomposition en produit de facteurs premiers.

Finalement M = m = PPCM(a, b)

Ouvrir le cours sur la divisibilité
Ouvrir l'article sur les nombres p-adiques
Consulter les notations

---

Auteur : Pascal Audoux
Relecteurs :Thomas Capricelli
Sources :

Cours de Mathématiques Supérieure de M. Coulet ( Saint-Louis HX5 94-95 )